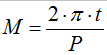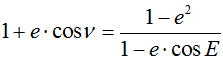La binaire spectroscopique beta Aurigae

Résumé

Grâce à la haute résolution du Lhires III, il est possible de séparer de nombreuses étoiles binaires spectroscopiques. Ces étoiles, qui n’apparaissent comme une seule étoile au télescope, montre un spectre dédoublé par l’effet Doppler. Nous décrivons ici dans le détail l’exemple de beta Aurigae avec des pistes pour d’autres cibles. Cet article a été originellement publié dans la revue AstroSurf et écrit en collaboration avec Pierre Noyrez pour la partie mathématique.

Beta Aurigae : une cible de choix ! Mais pas unique …

En 1783, John Goodricke (1765-1787) n’avait que 18 ans lorsqu’il fit un rapport à la Société Royale de Londres suggérant que les variations de luminosité d’Algol, qu’il avait observées, pouvaient être provoquées par un large compagnon. Il existe de nombreuses étoiles de type variable à éclipse parmi lesquelles (mais pas seulement) les RS Cvn, epsilon Aur, W UMa, et les Algols. Leur période de variabilité va de quelques dizaines de minutes à plusieurs années – l’étoile epsilon Aur étant dotée de la plus longue période connue et un système particulièrement intéressant à étudier (Sahade, 1993). Antonia Maury (1866-1952), qui a largement contribué à l’élaboration de la classification spectrale à l’observatoire de Harvard, s’est intéressée aux binaires spectroscopiques (Hearnshaw, 1986). Elle découvrit ainsi en 1889 la seconde binaire spectroscopique à Harvard: beta Aurigae. Rappelons pour l’anecdote son nom traditionnel «Menkalinan», ou «Menkarlina» ; ce dernier étant dérivé de l’arabe mankib ðī-l-‘inān, qui signifie « l’épaule du Cocher ».

La constellation du Cocher au dessus de la coupole de Saint-Véran (photo : Jan Karel Lameer)

Notre choix de beta Aurigae (A1 IV,  HR 2088, HD 40183, HIP 28360, Mv = 1.9, RA2000 = 05h59m31.7s, Dec2000 = 44°56’50.8’’) comme cible spectroscopique a été fait sur une liste d’étoiles binaires (SB9, 2004), essentiellement pour sa brillance et l’éclat proche des deux composantes, ainsi que la période assez courte de rotation.

En utilisant un spectroscope suffisamment résolvant, il est ainsi possible de distinguer le spectre de chacune des 2 composantes. Un pareil système est appelé binaire à deux spectres (notée BS2). Il se distingue d’une binaire à un spectre (BS1) pour laquelle seule la composante primaire la plus brillante serait observable. Notons qu’il est habituellement considéré qu’une différence d’éclat d’une magnitude entre la primaire et son compagnon rend la détection spectrale de ce dernier très difficile. beta Aurigae fait ici partie des bons exemples ! Le catalogue SB9 étant assez complet, on peut rechercher d’autres cibles – nombreuses dans le ciel – pour mener soi-même des projets similaires.

Acquisition des spectres et résultats

Les observations de beta Aurigae ont été menées sporadiquement entre le 22 août 2006 (lors d’un stage pratique spectroscopie de Planète Sciences) et le 20 octobre 2007. Toutes les observations ont été réalisées avec un spectrographe LHIRES-III équipé d’un réseau de 2400 traits/mm (pouvoir de résolution R= autour de 17000), par séries de trois poses de 5min. Certaines nuits, trois ou quatre séries ont été faites. L’objectif était d’avoir une bonne couverture de la phase de rotation de ce couple. Les observations sont le résultat de la collaboration entre Olivier Thizy (observations personnelles, CALA, AstroQueyras), François Cochard (observatoire du CALA), Jean-Pierre Masviel (CALA), Jose Ribeiro (AstroQueyras) et Eric Barbotin (observations personnelles).

Le Lhires III sur le C14 du CALA. François Cochard & Olivier Thizy dans la salle de contrôle…

En mode autoguidage, il n’y a pas grand-chose à faire !

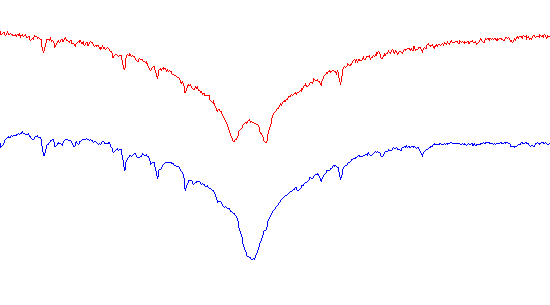
Exemple de spectre de beta Aurigae

La figure ci-dessus montre un exemple de spectre obtenu. Les raies fines sont des raies telluriques. Les deux raies larges au centre sont les raies Halpha des deux étoiles. Ce sont ces raies dont la position varie au cours du temps. Ainsi, le graphe et le spectrogramme suivant synthétisent l’évolution sur une période du spectre des deux composantes stellaires au voisinage de la raie Halpha ; la composante temporelle étant ici exprimée en fonction de la phase du système.

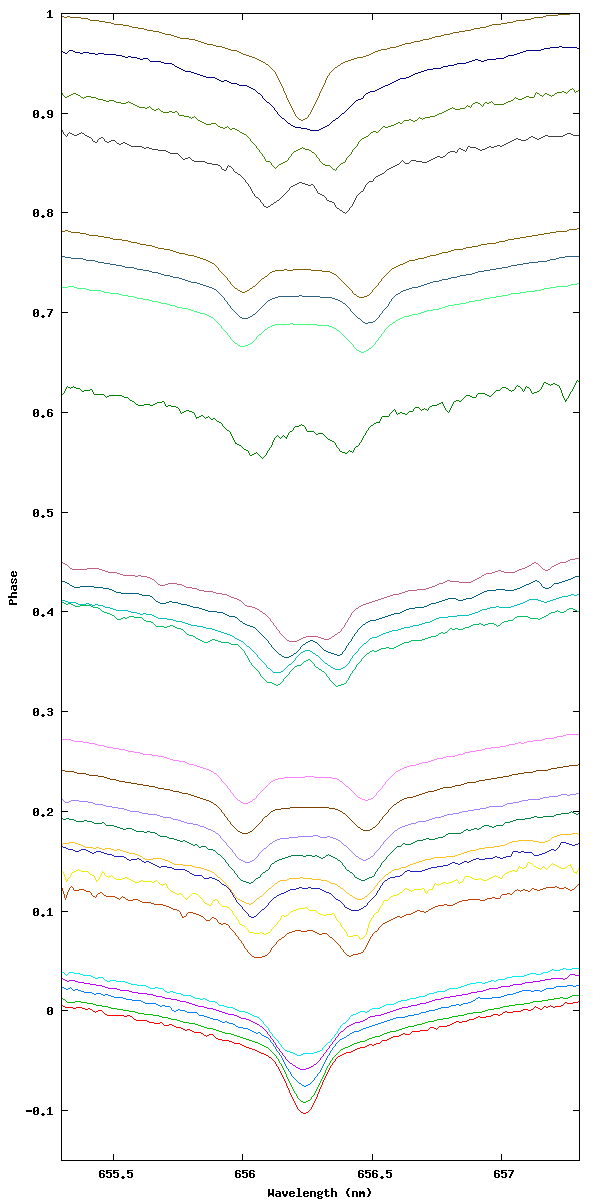
Evolution du spectre de beta Aurigae sur une période, le décalage sur l’axe Y est proportionnel à la phase de rotation.

L’évolution des décalages spectraux traduit les décalages Doppler-Fizeau observables par l’observateur terrestre du fait du mouvement des 2 étoiles autour de leur centre de masse commun; seules les composantes de vitesse projetées suivant la ligne de visée participant à la mesure. Ces dernières sont appelées «vitesses radiales».

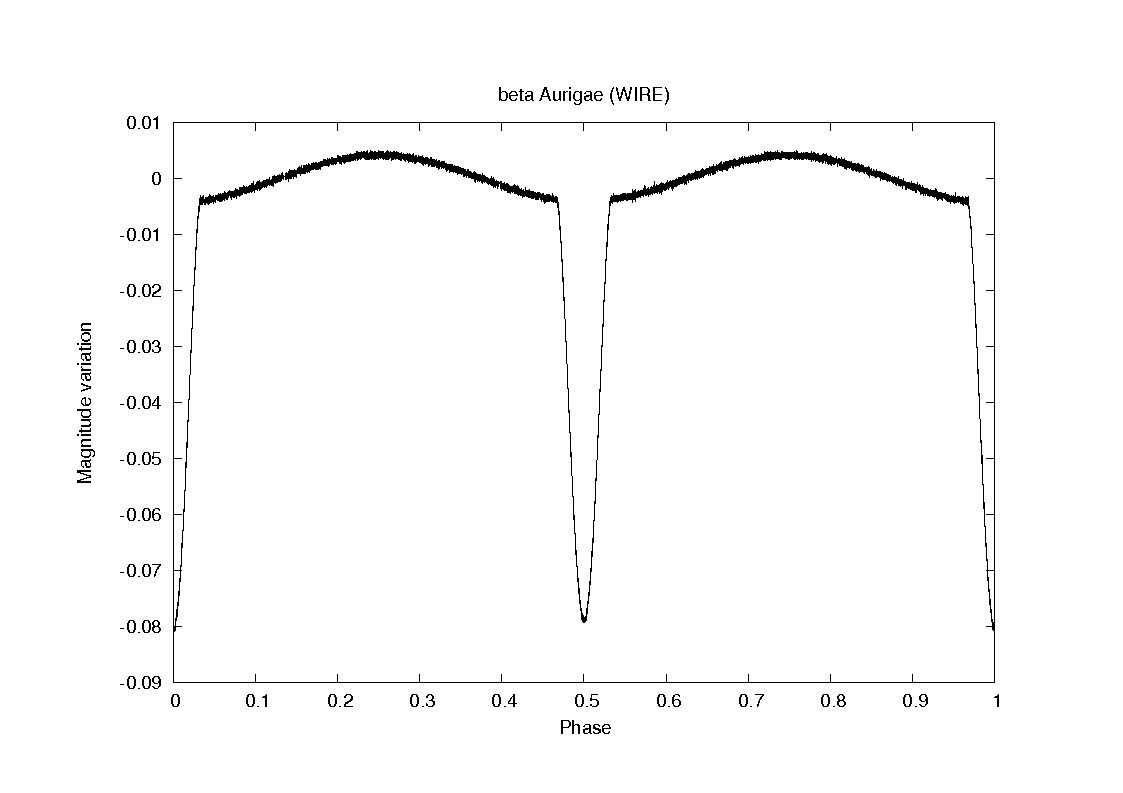
Rappelons que l’étoile beta Aurigae a été étudiée photométriquement notamment par le satellite WIRE (Southworth, 2007) dont la courbe photométrique confirme une période de 3.9600467300 jours. Pour chaque spectre obtenu, nous avons tout d’abord calculé le temps julien héliocentrique d’observation, c’est-à-dire le Jour Julien ramené au Soleil, et calculé une phase en utilisant cette période et une date arbitraire de début de phase HJD=2453827.19569.

Courbe de lumière de beta Aurigae (WIRE)

Aimez-vous les mathématiques ?

Il nous a semblé intéressant de rappeler le formalisme de base permettant de relier les données mesurables aux paramètres physiques orbitaux ; d’autant qu’en ce qui concerne les binaires spectroscopiques, ce formalisme est souvent éparpillé dans des ouvrages difficilement accessibles aux amateurs. Le lecteur assidu devrait donc trouver dans les paragraphes suivants les éléments lui permettant d’effectuer ces calculs lui-même, ou tout au moins acquérir les bases lui autorisant une bonne compréhension d’articles plus élaborés. Le lecteur pressé – quant à lui – pourra se satisfaire des simulations ludiques proposées par T. Herter et J. Köppen sous forme d’applet Java aux adresses Internet mentionnées en références. Quel que soit votre choix, ne manquez pas de visiter le dernier paragraphe afin d’accéder à la fin de l’histoire… via un logiciel téléchargeable gratuitement !

Les binaires ; une question de point de vue !

Lors de l’étude des systèmes doubles visuels, l’observateur étudie habituellement le mouvement d’une composante autour de l’autre, le référentiel adopté étant alors centré sur la composante la plus brillante (dite primaire) d’orientation fixe. Dans le cas – différent – des binaires astrométriques, l’observateur suit cette fois-ci le mouvement du photocentre autour du centre de masse du système. Les binaires spectroscopiques – quant à elles – s’étudient par l’intermédiaire des variations temporelles des vitesses radiales associées au mouvement des deux étoiles autour de leur centre de masse ; les courbes obtenues étant nommées ‘orbites spectroscopiques’. L’application de quelques lois physiques permet de calculer les paramètres fondamentaux de ces orbites.

Un peu de physique : les trois lois de Képler

Tout d’abord, l’application de la première loi de Képler aux étoiles doubles nous enseigne que chaque composante orbite autour du centre de masse (CDM) du système suivant une ellipse dont le CDM occupe l’un des foyers.

Changeons maintenant de point de vue en nous intéressant au mouvement relatif des deux composantes. L’orbite relative d’une composante (habituellement notée secondaire) autour de l’autre supposée fixe (dite primaire) est – par construction géométrique – une ellipse dont le demi grand axe a (respectivement demi petit axe b) est égal à la somme des demi grands axes ai (respectivement petit axes bi) des orbites individuelles autour du CDM.

Cette orbite relative est caractérisée par 7 éléments :

• a = demi grand axe,
• e = excentricité,
• P = période,
• Ω = angle de position du nœud par rapport au nord,
• ω = longitude du périastre par rapport au noeud,
• i = inclinaison du plan de l’orbite,
• T = époque de passage au périastre.

La seconde loi de Képler nous indique que la vitesse aréolaire est constante. En d’autres termes, la composante secondaire se déplace plus rapidement lorsqu’elle est proche de la composante primaire (maximale au périastre) que lorsqu’elle s’en trouve éloignée. Mathématiquement, si l’on note r la distance entre composantes ν et  l’angle polaire mesuré à partir du périastre (également appelé « anomalie vraie ») ; cela se traduit par la relation suivante :

La distance entre composantes r suit – quant à elle – la relation :

Enfin, la troisième loi de Kepler nous apprend que la masse totale du système M1+M2 (exprimée en masses solaires Msol) est liée au demi grand axe a (exprimé en unité astronomique UA) et à la période P (exprimée en année) par la relation :

Vitesses radiales ; variation temporelle sinusoïdale ou pas ?

Dans un système binaire, le mouvement orbital d’une étoile ajoute sa composante radiale Vr  sous la forme d’un terme périodique au terme constant de la vitesse radiale du centre de masse habituellement désignée Vr. L’application des deux premières lois de Kepler donne de ce fait l’équation suivante pour la vitesse radiale d’une composante :

La dépendance temporelle est ici cachée dans le terme V(t). On l’examinera plus en détail un peu plus loin.

La demi amplitude de la courbe de vitesse radiale Ki de chaque composante est – quant à elle – reliée à 4 paramètres orbitaux (le demi grand axe ai de l’orbite considérée autour du CDM, la période P, l’excentricité e et l’inclinaison i de l’orbite) par la relation suivante :

L’indice 1 désigne ici la composante primaire; l’indice 2 se rapportant à la secondaire (compagnon) lorsque celle-ci est détectable, bien entendu.

Il convient de noter ici que la relation (4) n’implique une variation temporelle sinusoïdale que dans le cas de trajectoires circulaires (c’est-à-dire à excentricité nulle) pour lesquelles  varie linéairement en fonction du temps (dans ce cas particulier,  V(t) = 2.π.t/P). Dans le cas plus général de trajectoires elliptiques, la variation temporelle peut présenter une asymétrie assez prononcée, qui traduit le fait que le déplacement est plus rapide au périastre. Son étude détaillée apporte de précieux renseignements sur les paramètres orbitaux (voir simulations en annexe).

Quels paramètres physiques accessibles ?

Dans le cas d’une binaires à deux spectres (BS2), les courbes Vr sont – à un facteur d’échelle près – inverse l’une de l’autre. Elle se croisent quant les vitesses des composantes sont égales à celle du centre de masse . Précisons qu’en vertu de la deuxième loi de Képler, pour chaque composante, l’aire de la courbe au-dessus de Vr est égale à l’aire en dessous de . Cette propriété est parfois exploitée afin de localiser graphiquement la position de Vt (cas des BS1). La mesure du rapport des amplitudes K1/ K2 autorise quant à elle la détermination directe de l’inverse du rapport des masses :

Précisons enfin, que dans le cas d’une BS1, seule la « fonction de masse » – notée f(M) – est accessible à l’observateur :

Cette « fonction de masse » permet une estimation de la masse minimale du compagnon.

Ici encore, les données physiques accessibles à l’observateur sont limitées à la projection sur l’axe de visée ; le sinus de l’inclinaison orbitale ne pouvant être déterminé par les mesures de vitesses radiales.

Le lecteur courageux – muni des ces quelques éléments de la physique des binaires – devrait maintenant être en mesure d’aborder avec confiance quelques articles plus élaborés. Nous le lui recommandons chaudement, le sujet étant passionnant et plus que jamais d’actualité puisque lié à l’étude des exo planètes. Leurs trajectoires suivent également le formalisme Képlérien. Mais avant cela, poursuivons notre étude de beta Aurigae.

Traitements appliqués aux spectres de beta Aurigae

Pour chaque spectre, nous avons mesuré l’écart de la position des raies des deux composantes par rapport à la position théorique de la raie Halpha (longueur d’onde centrale de 6562.88 Å) en tenant compte du décalage systématique lié à la vitesse de la Terre autour du Soleil (calculs réalisés par Olivier Thizy pour chaque observation avec la fonction HELIO du logiciel IRIS).

Précisons que deux approches séparées ont été tentées afin de mesurer les décalages spectraux. Dans la première, les minima des pics ont été évalués de manière directe grâce à la fonction ‘mesurer – centre raie’ du logiciel VSpec. Dans la seconde, les spectres prétraités, calibrés et corrigés des décalages héliocentriques ont été analysés (Pierre Noyrez) à l’aide d’un logiciel permettant la décomposition des pics (PeakFit) par technique de minimisation des résidus. Une soustraction préalable de la composante du continuum dite « ligne de base » a été effectuée par interpolation linéaire. Dans l’intervalle spectral couvert, les « ailes » larges ont été modélisées par des fonctions ‘lorentziennes’ (de largeur à mi-hauteur variable suivant la phase ; la valeur typique étant de l’ordre de 20.0 angströms). Les composantes primaires et secondaires ont chacune été modélisées par des ‘gaussiennes’ (largeur à mi-hauteur typique de l’ordre de 1.35 angström).

Précisons que les profils spectraux n’ayant pas été corrigés des effets d’élargissement instrumentaux (influence de la largeur de fente), l’élargissement des raies dû à la rotation propre de chaque composante n’est pas discuté dans cette étude. Nous nous sommes donc essentiellement attachés à mesurer la position des centroïdes de ces « gaussiennes » afin de quantifier les déplacements spectraux liés aux mouvements orbitaux des deux composantes.

Les déplacements spectraux  Δλ ainsi mesurés ont été traduits en termes de vitesses radiales par application de la loi Doppler-Fizeau :

Où c représente la vitesse de la lumière dans le vide et λ0 la longueur d’onde 6562.88 angströms.

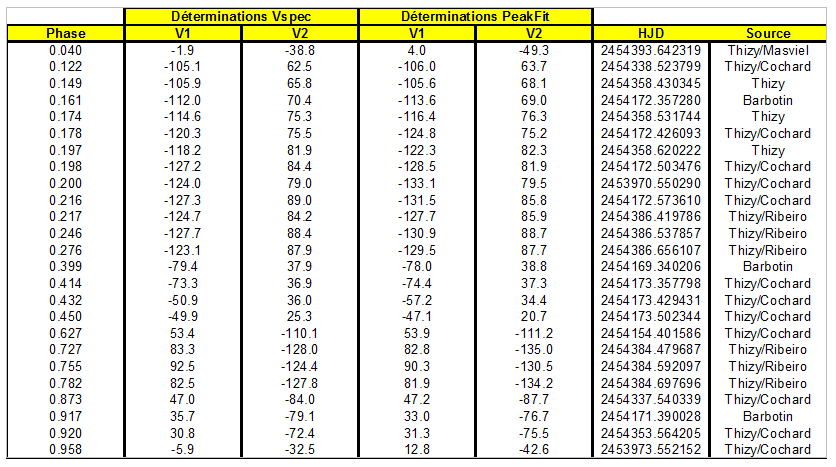
Les résultats obtenus ont été listés table 1. L’écart moyen constaté entre les deux méthodes était d’environ ½ pas, correspondant à environ 0.0575 angström, ce qui traduit un décalage en vitesse radiale de l’ordre de 3 km.s-1 approximativement (table 1), excepté au voisinage des positions éclipsées (phases proches de 0 et 1) où les raies deviennent difficiles à séparer.

Table 1 : Vitesses radiales en fonction de la phase pour chaque observation.

Les figures suivantes regroupent les valeurs ainsi mesurées pour chaque composante de la binaire en fonction de la phase du système :

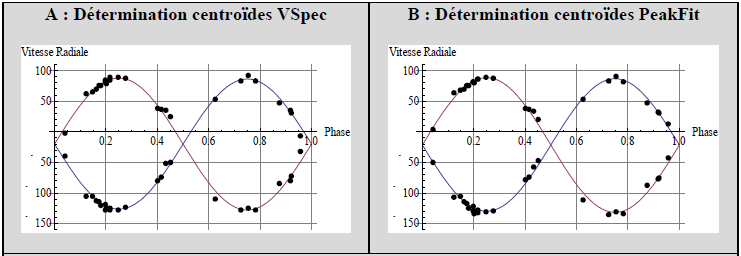
Graphe des vitesses radiales en fonction de la phase.

Comme indiqué précédemment, les courbes sinusoïdales traduisent des orbites quasi-circulaires autour du centre de masse du système. Les demi-amplitudes K1,2 sont du même ordre de grandeur, ce qui indique des masses très proches l’une de l’autre.

Le lecteur assidu enfin récompensé !

Conscient du fait que l’amateur ne dispose peut-être pas des outils de calcul permettant d’évaluer les paramètres orbitaux à partir des mesures de vitesses radiales, nous avons effectué une recherche sur la toile Web. Les astronomes professionnels utilisent généralement le code de calcul SBOP (Etzel 1985) ; malheureusement celui-ci ne nous est habituellement pas directement accessible.

Par contre, nous avons pu localiser, puis télécharger le logiciel gratuit ‘Spectroscopy Binary Solver (SBS)’. Son adresse web est citée en référence. SBS est un logiciel interactif graphique permettant la détermination de la période (lorsque inconnue), puis des paramètres orbitaux d’un système binaire (de type BS1 ou BS2) à partir des vitesses radiales mesurées expérimentalement. Ce logiciel a été écrit en langage Microsoft® Visual Basic par Delwin O. Johnson lors de ses études d’astronomie à l’université de San Diégo aux Etats-Unis. Nous le recommandons au lecteur, il est performant et facile d’utilisation.

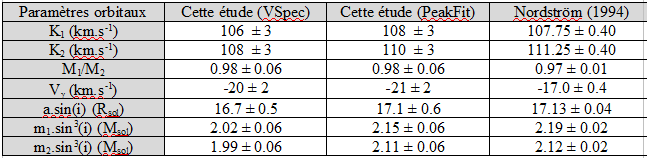
Les déterminations ci-dessous résultent des calculs effectués grâce au logiciel SBS. Elles sont à comparer aux mesures réalisées par Popper & Carlos, ainsi que Smith et citées par Nordström (1994).

Table 2 : Paramètres orbitaux déduits des mesures de vitesse radiales après calculs sous SBS.

L’accord est remarquable, excepté peut-être en ce qui concerne la vitesse  Vr du centre de masse du système dont le module semble être surévalué d’environ 20 % par rapport aux mesures rapportées par Nordström. Les valeurs obtenues sont toutefois en assez bon accord avec la valeur Vr =  -19.4 ± 1.0 km.s-1 rapportée par Popper & Carlos (1970).

D’autres cibles

Il existe de nombreuses autres cibles à faire avec des spectrographes comme le Lhires III ou le eShel. Même les exoplanètes sont à la portée du eShel de part la technologie échelle et la stabilité de l’instrumentation avec l’utilisation de la fibre optique.

Parmi les cibles, on notera par exemple :

•  Mizar : à faire sur plusieurs nuit; avantage d’être souvent (toujours!) visible dans l’hémisphère Nord et cible brillante.

• AW UMa : une étoile à contact à faire sur une nuit en hiver.
• beta Lyrae (lien vers les étoiles Be): à suivre sur trois semaines consécutive, avec un spectre en émission (étoile Be).

Conclusion

Ainsi que le montre cet article, l’amateur motivé peut réellement accéder à la mesure des paramètres physiques principaux d’une binaire spectroscopique, à supposer quelques conditions minimales. Précisons que le suivi régulier de systèmes déjà connus est très utile ; certains paramètres pouvant évoluer lentement dans le temps, révélant ainsi la présence d’un troisième compagnon ou encore les transferts de matière d’une étoile à l’autre. Nous avons tenté de donner au lecteur les outils lui permettant d’effectuer ses propres recherches. Nous espérons également lui en avoir communiqué l’envie. Alors, tous à vos spectros LHIRES-III !

ANNEXE – FORME GENERALE DE LA VITESSE RADIALE

Il est intéressant de rappeler que la modélisation de la dépendance temporelle de la vitesse radiale. Vr n’est pas si évidente qu’elle peut le paraître de prime abord, sauf dans le cas particulier d’orbites circulaires. Nous rappelons ici au lecteur intéressé qu’elle passe par quatre étapes successives :

1) calcul de l’anomalie moyenne M(t) :

2) calcul de l’anomalie excentrique E(t) en résolvant l’équation dite «de Képler» :

Cette équation est « transcendantale », elle ne peut pas être résolue analytiquement en E. Toutefois, elle admet une solution unique pour toute valeur de M non-multiple du nombre p. Vu son importance en mécanique céleste, plusieurs méthodes numériques ont été développées afin

d’autoriser sa résolution.

3) calcul de l’anomalie vraie n(t) en résolvant l’équation :

4) enfin, calcul de Vr(t) suivant l’expression :

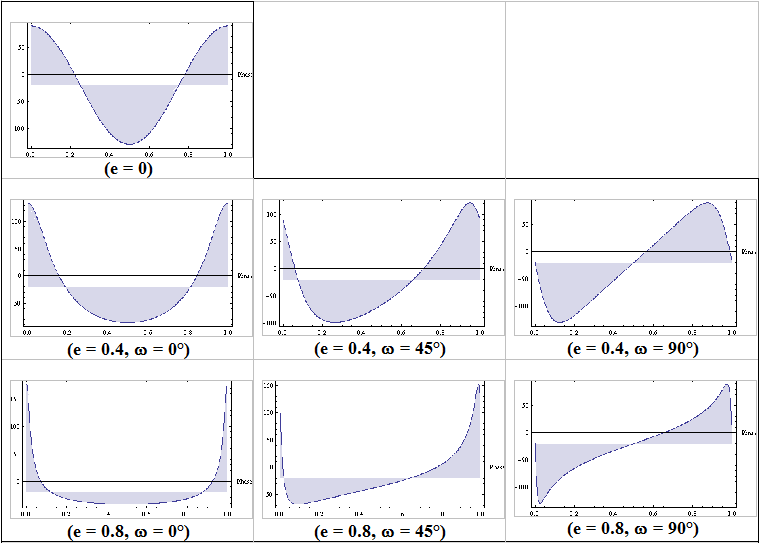
Le tableau ci-dessous présente quelques exemples de courbes de vitesse radiales (K = 110 km.s-1 ;  = -20 km.s-1) calculées par Pierre Noyrez sur une période en utilisant le formalisme décrit précédemment; les traitements numériques ayant été effectués en utilisant logiciel Mathematica® 6.

Courbes de vitesse radiale pour différentes valeurs de e et ω

Comme on peut le voir dans ce tableau, la forme de la courbe radiale donne de précieuses indications quant aux paramètres de l’orbite d’une binaire spectroscopique. La comparaison entre données expérimentales et courbes modélisées autorise d’ailleurs une première estimation des paramètres e et ω ; les paramètres définitifs étant habituellement ajustés numériquement de manière itérative afin de minimiser la différence quadratique moyenne entre valeurs calculées et mesurées. Enfin, on notera que le profil sinusoïdal n’est obtenu que pour des trajectoires circulaires.