Rotation de planètes

Équipement recommandé : Lhires III, eShel
Durée : une soirée (acquisition), 4h (analyse en groupe)

Introduction

L’effet Doppler-Fizeau est particulièrement visible sur un spectre de Jupiter ou Saturne pris avec un Lhires III. Un seul spectre de Jupiter suffit pour montrer l’inclinaisons des raies de la planète par rapport à celles de notre atmosphère. La haute résolution du Lhires III donne une bonne précision à la mesure du décalage entre les deux bords. Le spectrographe eShel peut également être utilisé pour ce projet.

Bien adapté pour des lycéens avec une partie pratique simple à réaliser et la partie théorie/analyse qui peut facilement prendre 1/2 journée pour comprendre le phénomène, ce projet permet de calculer la vitesse de rotation linéaire de la planète, ses dimensions, etc…

Cet article a été originellement publié dans la revue AstroSurf.

L’effet Doppler-Fizeau

L’analyse de la lumière des astres nous renseigne sur leur composition chimique, les conditions physiques telles la température, pression, gravité, etc… Mais le spectre contient aussi des informations de vitesse grâce à l’effet Doppler-Fizeau.

Pour des vitesses faibles (disons inférieures à 10 000 km/s), le décalage en longueur d’onde  est lié à la vitesse radiale Vr par la formule de Doppler-Fizeau:

où λ est la longueur d’onde mesurée en laboratoire et c la vitesse de la lumière dans le vide (constante: c=300 000 km/s). Autour de la raie Halpha, une vitesse de 50 km/s donne un décalage de 0,1nm (ou 1Å) environ. C’est un ordre de grandeur à garder en mémoire.

Le décalage se fait vers les longueurs d’onde plus grandes quand la source et l’observateur s’éloignent l’un de l’autre (décalage vers le rouge dans le domaine du visible) et à l’inverse se fait vers les longueurs d’onde plus petites quand ils se rapprochent (décalage vers le bleu). Le décalage dans le rouge (redshift en anglais) a connu son heure de gloire dans les années 1930 quand Hubble a pu mettre en évidence l’expansion de l’univers pas un décalage globalement vers le rouge des galaxies, d’autant plus élevé que les galaxies étaient lointaines de nous.

Attention car il s’agit de la vitesse radiale, c’est-à-dire la vitesse projetée sur la ligne de visée entre la source et l’observateur. La spectroscopie ne mesure pas les vitesses tangentielles, ou mouvements propres, qui sont mesurés par d’autres techniques: astrométrie par exemple. Il est à noter que les précisions obtenues en spectroscopie sur les mouvements radiaux sont très importantes, et ce quelque soit la distance de la source.

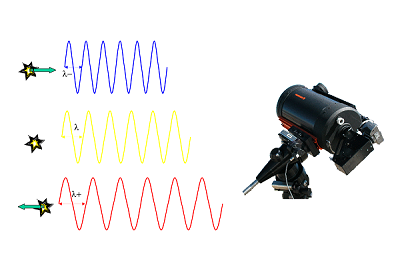
l’effet Doppler

Les planètes géantes comme Jupiter ou Saturne réfléchissent la lumière du Soleil. Leur spectre est donc assez proche de celui du spectre solaire avec quelques modifications (bandes de méthanes par exemple). Ces deux planètes ont la propriété d’être assez grandes et résolues avec des instruments d’amateur même de petite focale. On essayera toutefois d’utiliser un instrument de longue focale (4 mètres ou plus) afin d’avoir un spectre le plus large possible.

Jupiter

Une résolution spectrale importante est nécessaire pour détecter le décalage en longueur d’onde généré par la rotation de la planète. Le Lhires III, avec une résolution de 0.3Å, rend très facile cet exercice. Il est également possible de réaliser cet exercice avec un spectrographe eShel en prenant deux spectres: un sur chaque bord de la planète. Mais le spectrographe à fente Lhires III est toutefois plus adapté à ce projet.

Le spectre de Jupiter qui illustre cet article a été réalisé avec un C11 f/10, un Lhires III équipé du réseau de 2400 traits/mm. Ce spectrographe est muni d’une fente alors réglée à 30µm ce qui fait qu’une partie seulement de la lumière de la planète est décomposée. La fente est réfléchissante (on voit avec une webcam l’objet visé) ce qui a permis de l’aligner sur l’équateur de la planète.

spectre de Jupiter obtenu en 5min de pose seulement

Certaines raies du spectre sont inclinées. Cela est provoqué par la rotation de la planète: le bord qui s’approche de nous voit son spectre décalé vers le bleu par rapport au centre de la planète, par effet Doppler-Fizeau avec un décalage proportionnel à la vitesse linéaire. Le bord qui s’éloigne de la même façon voit son spectre décalé vers le rouge. A noter les autres raies présentes dans le spectre mais bien verticales: ce sont les raies d’absorption de l’atmosphère terrestre (raies telluriques); il est normal qu’elle ne soient pas inclinées puisque l’atmosphère est fixe par rapport à nous.

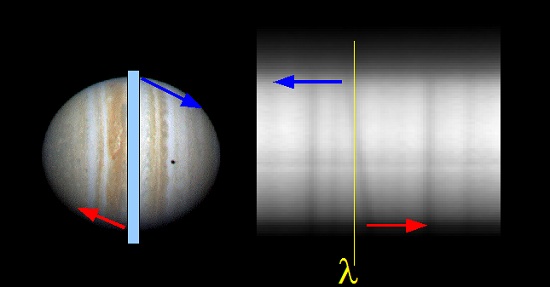
schéma de principe

La simplicité de cette mesure tient – outre le faible temps de pose et la facilité de pointer l’objet – au  fait que toute l’information est contenue dans l’image: c’est à l’inclinaison relative des raies de Jupiter par rapport à celles de l’atmosphère terrestre que l’on va s’attacher – il n’est même pas nécessaire de calibrer le spectre en longueur d’onde…

En mesurant le décalage Dl aux bords des raies inclinées, on peut calculer la vitesse linéaire au bord de la planète par rapport au centre de la planète par la formule :

Vr=¼ .c.Δλ / λ

Pourquoi le facteur ‘¼’ ? D’abord parce que la mesure est faite entre les deux bords, donc la vitesse est mesurée deux fois : une fois à chaque bord. Mais aussi parce que l’effet Doppler-Fizeau agit deux fois : une première fois quand la lumière du Soleil atteint le bord de la planète, et une deuxième fois quand la lumière en repart. Au total, l’effet Doppler-Fizeau agit donc quatre fois dans le cas d’un corps réfléchissant la lumière d’un autre astre.

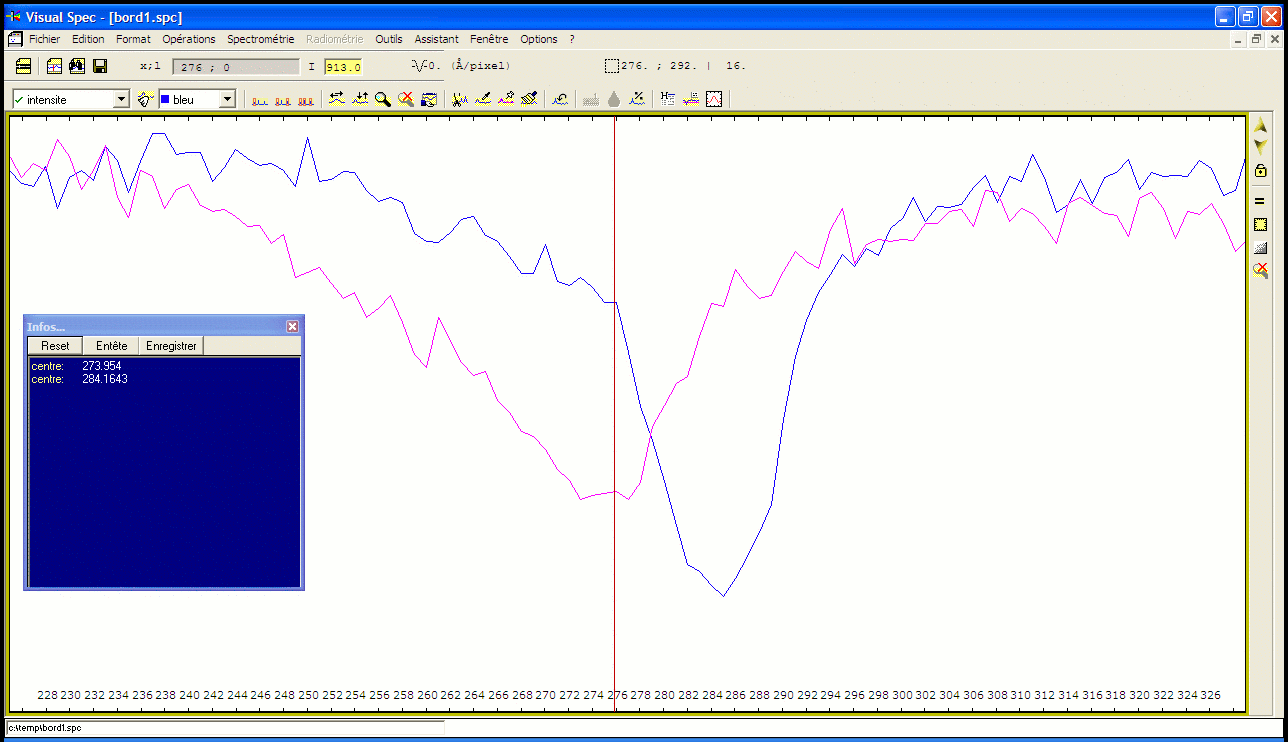
Sur le spectre de Jupiter, nous avons d’abord fait une coupe verticale pour trouver la position des bords: position 92 et 224 dans notre exemple.

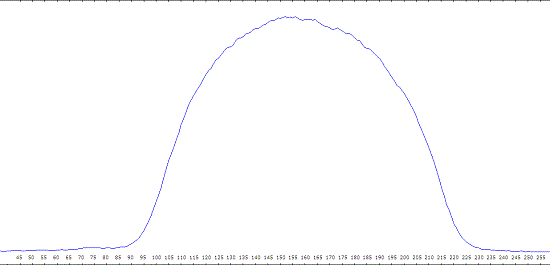
Coupe verticale du spectre de Jupiter

Mesure de l’écart entre les raies des deux bords de Jupiter (cliquer pour agrandir)

Puis nous avons pris chaque ligne des bords et mesuré, avec VisualSpec, la position de la raie Ha; le décalage mesuré est mesuré à 10.2 pixels avec une dispersion de 0.0115 nm/pixel. Soit donc une vitesse linéaire à l’équateur de Jupiter de:

v =  ¼ * 300 000 * 10.2 * 0.0115 / 656.3 = 13.4 km/s

Connaissant maintenant la vitesse de rotation de la surface de Jupiter, on peut pousser le raisonnement un peu plus loin. Sachant que la période de rotation de la planète fait P=9.84h (cela s’observe visuellement en suivant la rotation de la tâche rouge par exemple), on calcule le diamètre de Jupiter D:

D = v.P / π = 13.4*9.84*3600/3.1415 = 151 100 km

La valeur est proche de celle donnée dans les encyclopédies: D=140 000 km. La différence provient d’une fente qui n’était pas exactement alignée avec l’équateur de Jupiter (inclinaison de la planète) et bien entendu de la précision de la mesure.

Les plus curieux d’entre vous pourront aller encore plus loin : la période de rotation des satellites nous permet de remonter à la masse de la planète (3ème loi de Kepler). Comme on connait maintenant le diamètre de la planète, on peut en déduire son volume, puis sa densité…

Saturne

De l’image de Saturne au spectre

L’exercice est similaire pour Saturne avec en prime le spectre, donc la vitesse, des anneaux. Ceci est illustré par le spectre pris par Christian Buil avec un Lhires III et un Appareil Photographique Numérique dans la région infra-rouge. Les raies fines du spectre solaire, inclinées, sont bien visibles ainsi que des bandes larges sur la planète mais pas sur les anneaux: ce sont les bandes du méthane de Saturne.

Spectre de Saturne en proche Infra-Rouge (par Christian Buil)

Le spectre qui va nous servir au calcul de la rotation a lui été pris à l’observatoire du CALA avec un Lhires III (2400 traits/mm, C14 f/10, caméra CCD Audine KAF400).

Spectre de Saturne (Lhires III)

Sur la planète uniquement, la mesure du décalage en longueur d’onde est de 8.33 pixels avec une dispersion toujours de 0.0115 nm/pixel. On en déduit la vitesse linéaire à l’équateur:

v = ¼*300 000 * 8.33 * 0.0115 / 656.3 = 10.9 km/s

La période de rotation de Saturne est plus difficile à mesurer mais peut être faite lorsque un cyclone apparaît à sa surface. Elle est de 10.66h. D’où le diamètre de Saturne:

D = v.P / π = 10.9 * 10.66 * 3600 / 3.1415 = 133 000 km

La valeur calculée est assez proche des 120 000 km donnés dans les encyclopédies.

Le spectre des anneaux est différent de la planète, on voit clairement une brisure dans la pente des raies en absorption. En effet, le décalage des raies sur Saturne, donc la vitesse, est linéaire en fonction de la distance au centre de la planète. C’est le signe que la planète tourne comme un corps solide (avec la précision de nos mesures). Par contre, les anneaux ont une vitesse constante (toujours à la précision de nos mesures) quelque soit la distance à la planète. En fait, une précision plus grande montrerait que les anneaux tournent de façon képlerienne car ils ne sont pas solides; c’est un ensemble de petits corps qui suivent la loi:

a3/T2=Cte

Conclusions

L’observation que nous venons de décrire est intéressante à plusieurs titres, pour qui démarre en spectroscopie:

– c’est une observation qui prend très peu de temps : quelques minutes de poses suffisent, les objets sont très brillants

– c’est une observation simple: toute l’information est contenue dans une seule image; pas besoin de calibrer précisément en longueur d’onde

– le résultat est impressionnant… allez dire à vos amis que vous avez mesuré la vitesse de rotation de Saturne… effet garanti !

C’est un magnifique support pédagogique : nous avons là une expérience facile à conduire avec des lycéens, des étudiants ou dans un club d’astronomie, et qui couvre aussi bien la partie technique (observation, traitement des images) que la partie scientifique (mesure des décalages dans l’image, calcul de la rotation…). Vous pouvez même pousser la rigueur jusqu’à utiliser les statistiques pour améliorer la précision des mesures. C’est donc une petite mise en bouche spectaculaire… nous vous encourageons vivement à faire cette expérience avec votre propre matériel !